ANSI/TIA/EIA-568-B Estándar de cableado de telecomunicaciones en edificios comerciales - Luis Gómez

 ANSI/TIA/EIA-568-B 

Estándar de cableado de telecomunicaciones en edificios comerciales

ANSI

    Es una organización privada sin fines de lucro que administra y coordina los estándares voluntarios y el sistema de evaluación de la conformidad de los EE. UU. Fundado en 1918 , el Instituto trabaja en estrecha colaboración con las partes interesadas de la industria y el gobierno para identificar y desarrollar soluciones basadas en estándares y conformidad para las prioridades nacionales y globales.

TIA

    La Asociación de la Industria de las Telecomunicaciones (TIA, por sus siglas en inglés) se encuentra en el centro para garantizar un rendimiento, una seguridad y una sostenibilidad óptimos de las Tecnologías de la Información y las Comunicaciones (TIC) de última generación al reunir a las comunidades de interés para dar forma a soluciones que toquen todos los aspectos del mundo conectado digitalmente.

EIA

La Alianza de Industrias Electrónicas, conocida hasta 1997 como Electronic Industries Association, es una organización que está formada por la asociación de las compañías electrónicas y de alta tecnología de Estados Unidos. Su misión es promover el correcto desarrollo del mercado, así como la competitividad de la industria de la alta tecnología de Estados Unidos con el apoyo local e internacional de la política.

ESTANDAR DE CABLEADO ESTRUCTURADO

Fue creado para:

• Establecer especificaciones de cableado que soporten las aplicaciones de diferentes vendedores.
• Brindar una guía para el diseño de equipos de telecomunicaciones y productos de cableado para sistemas de telecomunicaciones de organizaciones comerciales.
• Especificar un sistema general de cableado suficiente para soportar aplicaciones de datos y voz.
• Proveer pautas para la planificación e instalación de sistemas de cableado estructurado.

SUBSISTEMAS DE CABLEADO ESTRUCTURADO

La norma ANSI/TIA/EIA 568-B divide el cableado estructurado en siete subsistemas, donde cada uno de ellos tiene una variedad de cables y productos diseñados para proporcionar una solución adecuada para cada caso. Los distintos elementos que lo componen son los siguientes:

1. Subsistema de cableado Horizontal
2. Área de Trabajo
3. Subsistema de cableado Vertical
4. Cuarto de Telecomunicaciones
5. Cuarto de Equipos
6. Cuarto de Entrada de Servicio
7. Subsistema de Administración

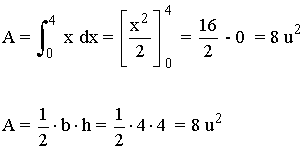
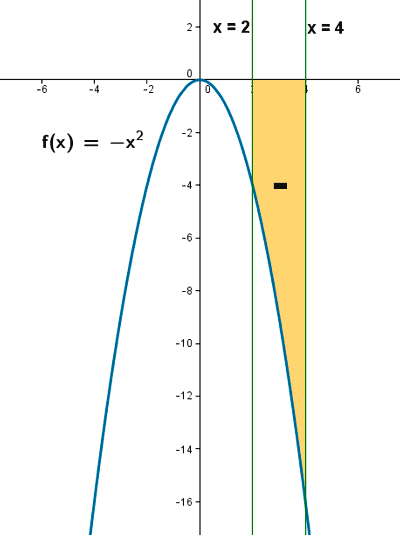
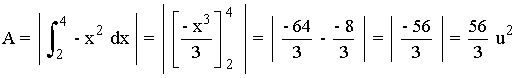
CARACTERISTICAS DE LOS SUBSISTEMAS 

BIBLIOGRAFÍA:

https://www.ansi.org/about/introduction

https://tiaonline.org/what-we-do/

https://atlascomunicaciones.com/norma-eia/

http://bracamontedatacenters.weebly.com/cableado-estructurado.html

CÁLCULO INTEGRAL - ÁREAS CURVAS, PLANAS, COORDENADAS POLARES - TEOREMA DE L´HOPITAL

 ÁREAS CURVAS

Supongamos que f (x) y g(x) sean funciones continuas tales que f (x) ≥ g(x) en un intervalo [a, b]. Supongamos que R denota la región delimitada arriba por la gráfica de f (x), abajo por la gráfica de g(x), y a la izquierda y derecha por las rectas x = a y x = b, respectivamente. Entonces, el área de R viene dada por:

EJEMPLO

Si R es la región acotada arriba por la gráfica de la función f (x) = x + 4 y abajo por la gráfica de la función g(x) = 3 − x/2 en el intervalo [1, 4], encuentre el área de región R.

SOLUCIÓN:

La región se muestra en la siguiente figura.

El área de la región es de 57/4 unidades

ÁREAS PLANAS

La función    f(x)    es positiva en el intervalo    [a, b]

Hallar por integración el área del triángulo formado por la bisectriz del primer cuadrante al eje    OX    y la recta   x = 4 .  Comparar el resultado con el que se obtiene geométricamente.

La función    f(x)    es negativa en el intervalo    [a, b]

Hallar el área del recinto limitado por la parábola de la ecuación    y = - x²  ,    el eje    OX    y las rectas    x = 2    y    x = 4 .

ÁREA EN COORDENADAS POLARES:

Las coordenadas polares o sistema de coordenadas polares son un sistema de coordenadas bidimensional en el que cada punto del plano se determina por una distancia y un ángulo. Este sistema es ampliamente utilizado en física y trigonometría.

De manera más precisa, como sistema de referencia se toma: (a) un punto O del plano, al que se llama origen o polo; y (b) una recta dirigida (o rayo, o segmento OL) que pasa por O, llamada eje polar (equivalente al eje x del sistema cartesiano).

TEOREMA DE L´HOPITAL

Para poder aplicar la regla de L'Hôpital hay que tener un límite de la forma , y tener una de las siguientes determinaciones

• ,
• 
• 
  
• EJEMPLO
  

  

  
  

  
  

SUCESIONES - CALCULO INTEGRAL

DEFINICIÓN DE SUCESIÓN:

Es una serie de elementos , finita o infinita que se siguen unos detrás de los otros en el tiempo o en el espacio obedeciendo un orden.

CONVERGENCIA Y SU LIMITE:

Sucesión convergente

Una sucesión a(n) es convergente cuando tiene límite finito. El límite L  de una sucesión a(n) es el número al que la sucesión se aproxima cada vez más. Se dice que la sucesión a(n) converge a su límite L  y se expresa por:

SUCESIONES MONÓTONAS:

Se divide en dos tipos de sucesiones monótonas que son:

La Sucesión Creciente:

Una sucesión a(n) es monótona creciente  cuando cada término es mayor o igual que el anterior:

EJERCICIO DE UNA SUCESIÓN CRECIENTE:

La sucesión $a_n=2n$ es estrictamente creciente. Sus primeros términos son

Representación de la sucesión ($n$$\le 50$):

La Sucesión Decreciente:

Una sucesión a(n) es monótona decreciente cuando cada término es menor o igual que el anterior:

EJERCICIO DE SUCESIÓN DECRECIENTE:

La sucesión a(n) = 1 + 3/n es estrictamente decreciente:

Notación de sumatoria y propiedades.

El operando matemático que nos permite representar sumas de muchos sumados, n  o incluso infinitos sumados está expresado con la letra griega sigma (sigma mayúscula, que corresponde a nuestra S de "suma" ). La notación sigma es de la siguiente manera:

Esto se lee: Sumatorio sobre i, desde m hasta n, de x sub-i.

La variable i es el índice de suma al que se le asigna un valor inicial llamado límite inferior, m. La variable i recorrerá los valores enteros hasta alcanzar el límite superior, n. Necesariamente debe cumplirse que:

 

Propiedades

1) Cuando el límite inferior sea un entero mayor que 1, la cantidad de términos  (sumados) de una sumatoria se obtiene haciendo: límite superior (n) menos límite inferior (a) más la unidad(1):

  2) La sumatoria de una constante (k) es igual al producto (la multiplicación) entre dicha constante (k)  y  la cantidad de sumados (términos) :

3) La suma del producto de una constante (k) por una variable (x), es igual a k veces la sumatoria de la variable.

EJERCICIO:

BIBLIOGRAFÍA:

https://www.geogebra.org/m/vgmuAr2S

https://blogs.ua.es/matesfacil/progresiones-o-sucesiones/sucesion-monotona/

http://cidecame.uaeh.edu.mx/lcc/mapa/PROYECTO/libro5/341_notacin_de_sumatoria_y_propiedades.html#:~:text=La%20notaci%C3%B3n%20sigma%20es%20de,%2C%20de%20x%20sub%2Di.&text=3)%20La%20suma%20del%20producto,la%20sumatoria%20de%20la%20variable.