SUCESIONES: septiembre 2020

ÁREAS CURVAS

Supongamos que f (x) y g(x) sean funciones continuas tales que f (x) ≥ g(x) en un intervalo [a, b]. Supongamos que R denota la región delimitada arriba por la gráfica de f (x), abajo por la gráfica de g(x), y a la izquierda y derecha por las rectas x = a y x = b, respectivamente. Entonces, el área de R viene dada por:

EJEMPLO

Si R es la región acotada arriba por la gráfica de la función f (x) = x + 4 y abajo por la gráfica de la función g(x) = 3 − x/2 en el intervalo [1, 4], encuentre el área de región R.

SOLUCIÓN:

La región se muestra en la siguiente figura.

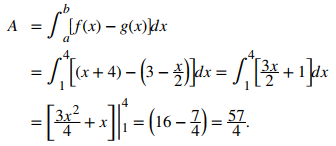
El área de la región es de 57/4 unidades

ÁREAS PLANAS

La función f(x) es positiva en el intervalo [a, b]

Hallar por integración el área del triángulo formado por la bisectriz del primer cuadrante al eje OX y la recta x = 4 . Comparar el resultado con el que se obtiene geométricamente.

La función f(x) es negativa en el intervalo [a, b]

Hallar el área del recinto limitado por la parábola de la ecuación y = - x², el eje OX y las rectas x = 2 y x = 4 .

ÁREA EN COORDENADAS POLARES:

Las coordenadas polares o sistema de coordenadas polares son un sistema de coordenadas bidimensional en el que cada punto del plano se determina por una distancia y un ángulo. Este sistema es ampliamente utilizado en física y trigonometría.

De manera más precisa, como sistema de referencia se toma: (a) un punto O del plano, al que se llama origen o polo; y (b) una recta dirigida (o rayo, o segmento OL) que pasa por O, llamada eje polar (equivalente al eje x del sistema cartesiano).

TEOREMA DE L´HOPITAL

$\displaystyle \lim_{x\rightarrow a}\frac{f(x)}{g(x)}=\lim_{x\rightarrow a}\frac{f'(x)}{g'(x)}$

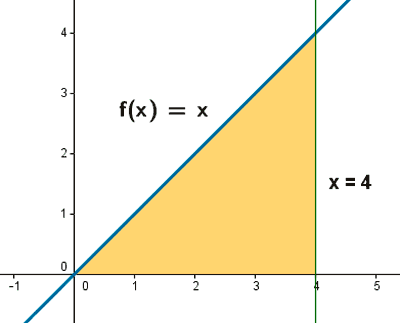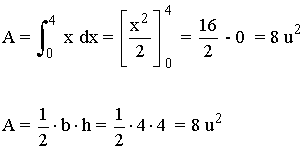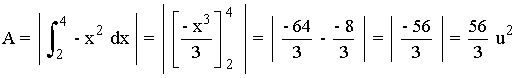
Para poder aplicar la regla de L'Hôpital hay que tener un límite de la forma $\displaystyle \lim_{x\rightarrow a}\frac{f(x)}{g(x)}$ , y tener una de las siguientes determinaciones